https://www.acmicpc.net/problem/1018
문제
지민이는 자신의 저택에서 MN개의 단위 정사각형으로 나누어져 있는 M×N 크기의 보드를 찾았다. 어떤 정사각형은 검은색으로 칠해져 있고, 나머지는 흰색으로 칠해져 있다. 지민이는 이 보드를 잘라서 8×8 크기의 체스판으로 만들려고 한다.
체스판은 검은색과 흰색이 번갈아서 칠해져 있어야 한다. 구체적으로, 각 칸이 검은색과 흰색 중 하나로 색칠되어 있고, 변을 공유하는 두 개의 사각형은 다른 색으로 칠해져 있어야 한다. 따라서 이 정의를 따르면 체스판을 색칠하는 경우는 두 가지뿐이다. 하나는 맨 왼쪽 위 칸이 흰색인 경우, 하나는 검은색인 경우이다.
보드가 체스판처럼 칠해져 있다는 보장이 없어서, 지민이는 8×8 크기의 체스판으로 잘라낸 후에 몇 개의 정사각형을 다시 칠해야겠다고 생각했다. 당연히 8*8 크기는 아무데서나 골라도 된다. 지민이가 다시 칠해야 하는 정사각형의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 M이 주어진다. N과 M은 8보다 크거나 같고, 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
출력
첫째 줄에 지민이가 다시 칠해야 하는 정사각형 개수의 최솟값을 출력한다.
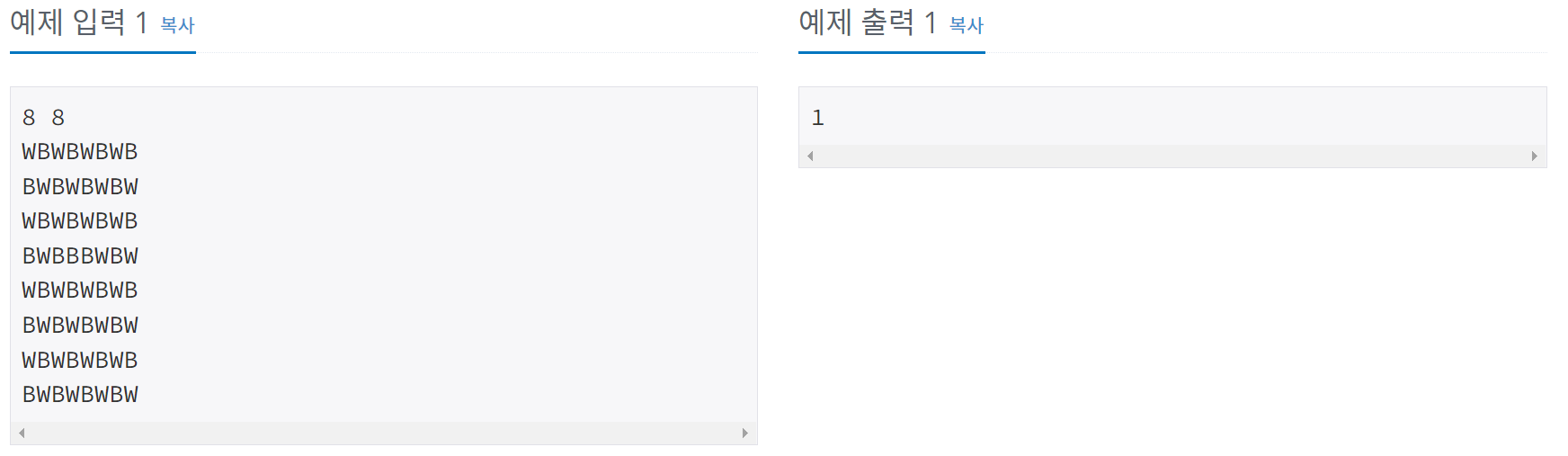
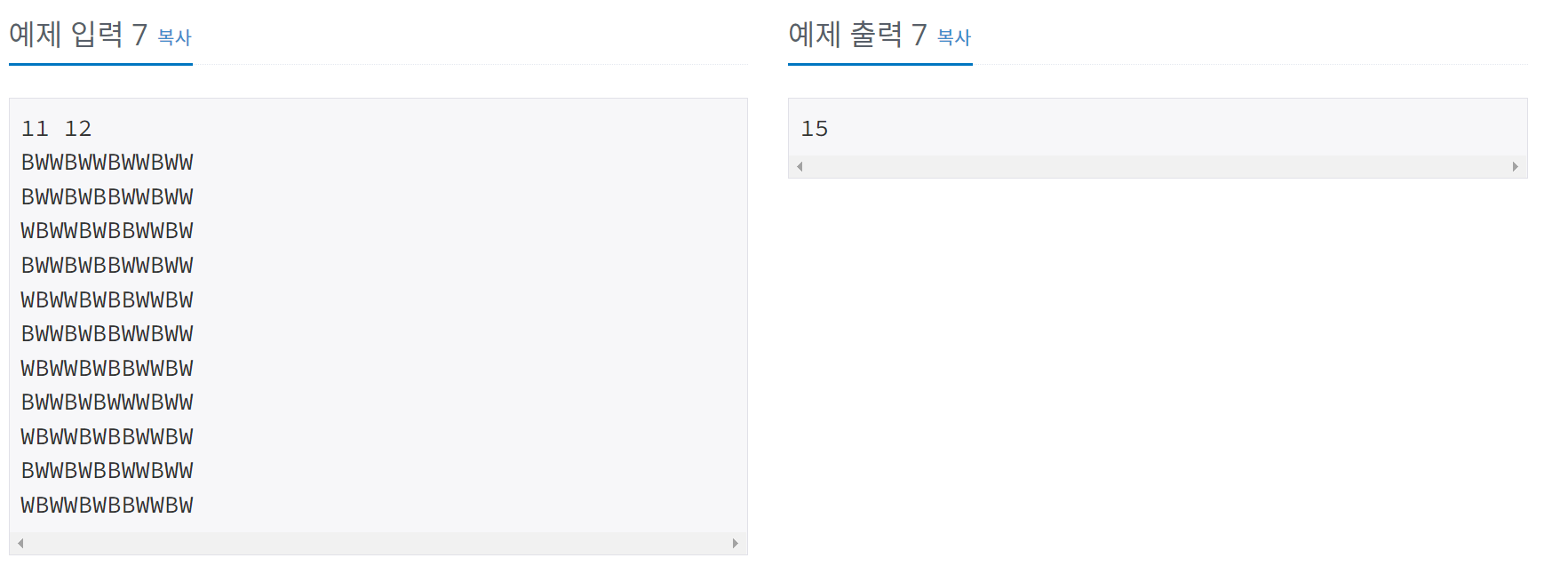
이 문제는 8 x 8 체스판을 최소한으로 만들려면 몇 칸을 다시 칠해야 하는가에 대한 문제이다.
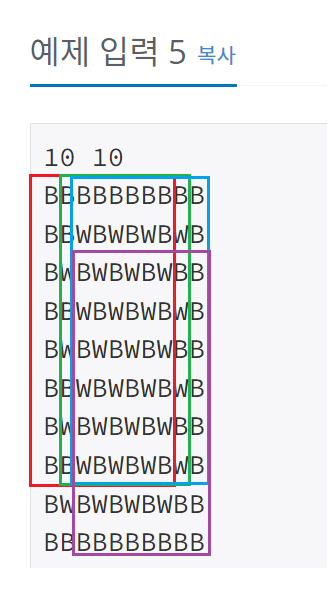
빨간 박스의 8x8 부터 시작해서 초록색 박스 파란박스를 하고 그 다음 계속 반복해서 보라색 박스의 8x8 까지의
모든 경우의 수를 찾는 브루트 포스 알고리즘 문제이다.
단순히 모든 경우의 수를 반복해야 하며 2차원 배열의 최대 8x8의 배열을 찾아야 하기 때문에 많은 반복문을 반복하게 된다.
우선 코드로 보면
n, m = map(int, input().split())
data = []
for i in range(n):
data.append(input())
cnt = 9999999
tmp = 0
for i in range(n-7):
for j in range(m-7):
case1 = 0
case2 = 0
for q in range(i, i+8):
for w in range(j, j+8):
if (q+w) % 2 == 0:
if data[q][w] != 'B':
case1 += 1
if data[q][w] != 'W':
case2 += 1
else:
if data[q][w] != 'W':
case1 += 1
if data[q][w] != 'B':
case2 += 1
tmp = min(case1, case2)
if cnt > tmp:
cnt = tmp
print(cnt)
정답 코드는 위와 같다.
문제를 풀기위해선 다음의 과정을 거쳐야 한다.
- 8 x 8 크기의 배열만 확인하면서
- 처음 시작은 'B' 혹은 'W로 시작할 수 있기에 두 가지 경우의 수를 모두 확인해야 한다.
- 모든 경우의 수를 찾아서 가장 최소의 값만을 찾아낸다.
우선

8 x 8의 배열만큼만 확인해야 하기 때문에
주어진 값에서 -7을 한 만큼만 반복문을 돌려 8x8 만큼의 배열을 최소한으로 확인하도록 한다.
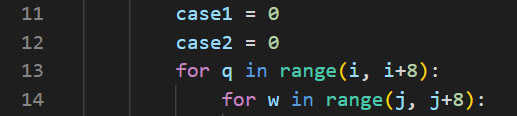
이후 처음 시작이 'B'인 경우와 'W'인 경우 두 가지의 경우의 수 모두를 고려하기위해
cas1과 case2 를 i j 반복문 내부에 선언하고
i~ i+8만큼의 8x8을 전부 순회하기 위해 다시 2차원 배열 2중 반복문을 선언해 준다.

아래 코드에서 확인할 수 있듯이
case1 은 처음 시작이 'B'일때 / case2 는 처음 시작이 'W'일 때로 정하여서
2중 반복문 내부에서 두가지 경우의 수를 모두 구해준다.

이후 가장 작은 값을 찾아서
처음 선언한 cnt에 값을 비교하여 넣어준 후
마지막에 모든 반복문을 탈출한 이후 최소값을 출력해준다.
이 문제는 머리로는 이해를 했으나
어느정도 시간이 지난 후 이 문제를 다시 풀라고하면 풀기 힘들것 같다.
아직 경험이 부족한건지 어떻게 풀어야 하는지 알면서도 도저히 코드를 적을 수가 없었고 결국에는
다른 사람의 코드를 참고하여 푼 문제이다.
'Algorithm > 백준' 카테고리의 다른 글
| [Python] 백준 9012번 - 괄호 (0) | 2022.10.21 |
|---|---|
| [Python] 백준 1920번 - 수 찾기 (0) | 2022.10.20 |
| [Python] 백준 11866번 - 요세푸스 문제 0 (0) | 2022.10.18 |
| [Python] 백준 11650번 - 좌표 정렬하기 (0) | 2022.10.17 |
| [Python]백준 10814번 - 나이순 정렬 (0) | 2022.10.15 |




댓글