문제 설명
N 가지 종류의 화폐가 있다. 이 화폐들의 개수를 최소한으로 이용해서 그 가치의 합이 M원이 되도록 하려고 한다. 이때 각 화폐는 몇 개라도 사용할 수 있으며, 사용한 화폐의 구성은 같지만 순서만 다른 것은 같은 경우로 구분한다. 예를 들어 2원, 3원 단위의 화폐가 있을 때는 15원을 만들기 위해 3원을 5개 사용하는 것이 가장 최소한의 화폐 개수이다.
입력 조건
- 첫째 줄에 N, M이 주어진다. (1 ≤ N ≤ 100, 1 ≤ M ≤ 10,000)
- 이후 N개의 줄에는 각 화폐의 가치가 주어진다. 화폐 가치는 10,000 이하 자연수
출력 조건
- 첫째 줄에 M원을 만들기 위한 최소한의 화폐 개수를 출력한다.
- 불가능할 때는 -1을 출력한다.

각 주어진 화폐 단위별 최적의 수를 찾으면 된다.
dp 테이블은 각 화폐단위별 최적의 수를 저장하고
없을 때는 나올 수 없는 수인 0~10,000 범위를 제외한 아무 값을 넣어준다.
우선 내가 작성한 코드를 보면
# 8-8 DP 효율적인 화폐 구성
import sys
n, m = map(int, sys.stdin.readline().split())
money = []
for _ in range(n):
money.append(int(sys.stdin.readline()))
dp = [10001] * (m+1)
dp[0] = 0
for i in range(1, m+1):
if i in money:
dp[i] = 1
else:
for j in range(n-1, -1, -1):
if i - money[j] < 0:
continue
else:
if dp[i-money[j]] != 10001:
dp[i] = dp[i-money[j]] + 1
break
if dp[m] == 10001:
print(-1)
else:
print(dp[m])

우선 dp테이블을 10,001로 초기화해주고
돈이 없는 경우인 d[0]은 0으로 초기화를 시켜준다.
이제부턴 점화식을 찾아야 한다.
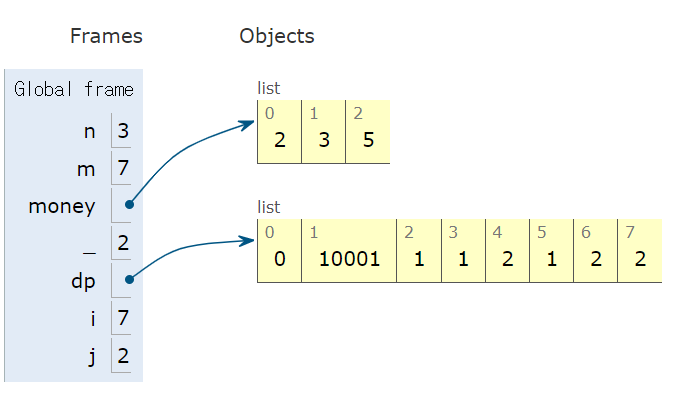
예를 들어서 dp[4]의 값을 찾는다고 할 때
우선 money에 4 값이 있는지 확인한다.
없다면 dp[4 - money[j]] 로
높은 금액 순서대로
dp[4 - 5] -> 에러 발생함으로 i - money[j] < 0 일 경우는 걸러준다.
dp[4 - 3] -> dp[1] = 10001 -> 값없음
dp[4 - 2] -> dp[2] = 1 (값 있음) 이후 dp[2] + 1을 해준 값을 dp[i]에 저장하여 준다.
즉 dp[4] = dp[4 - 2] + 1의 샘이 되는 것
이후 dp[5] 는 money에 5 값이 있기에 그대로 dp[5] = 1
dp[6]
dp[6 - 5] = 10001 (값없음)
dp[6 - 3] = dp[3] = 1 (값있음) + 1 = 2 -> break (가장 큰 경우의 수가 최소의 경우의 수이기 때문)
dp[7]
dp[7 -5] = dp[2] = 1 (값있음) + 1 = 2 -> break
위와 같은 방식으로 굴러간다는 것을 알 수 있다.
이후 저자의 정답 코드이다.
# 정수 N, M을 입력받기
n, m = map(int, input().split())
# N개의 화폐 단위 정보 입력받기
array = []
for i in range(n):
array.append(int(input()))
# 한 번 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [10001] * (m+1)
#DP 진행(bottom-up)
d[0] = 0
for i in range(n):
for j in range(array[i], m+1):
if d[j - array[i]] != 10001: # (i - k) 원을 만드는 방법이 존재하는 경우
d[j] = min(d[j], d[j - array[i]] + 1)
if d[m] == 10001:
print(-1)
else:
print(d[m])'Algorithm > 이것이 코딩테스트다' 카테고리의 다른 글
| [Python][이코테] 최단경로 / 다익스트라 알고리즘(2) (0) | 2022.11.15 |
|---|---|
| [Python][이코테] 최단경로 / 다익스트라 알고리즘(1) (0) | 2022.11.09 |
| [Python][이코테] 바닥 공사 / DP (0) | 2022.10.26 |
| [Python][이코테] 개미 전사 / DP (0) | 2022.10.25 |
| [Python][이코테] 1로 만들기 / DP (0) | 2022.10.23 |



댓글