https://www.acmicpc.net/problem/1929
1929번: 소수 구하기
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
www.acmicpc.net
문제
M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 M과 N이 빈칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
출력
한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.
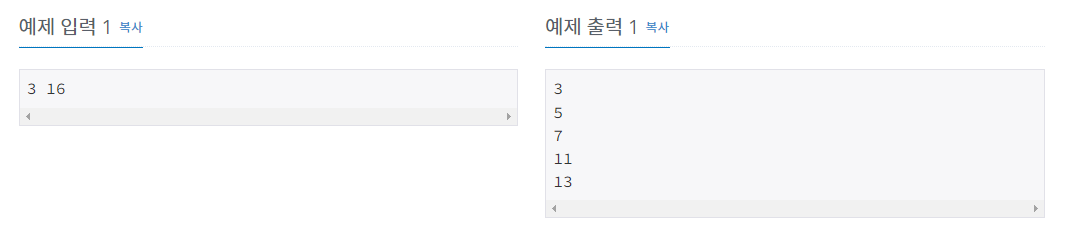
주어진 범위 안에서 모든 소수를 찾는 간단한 문제이다.
소수를 찾는방법에는 여러 가지 방법이 있다.
그중 가장 쉽게 떠올릴 수 있는 방법은
주어진 수를 처음부터 끝까지 검사하는 방법으로
import sys
m, n = map(int, sys.stdin.readline().split())
def find_prime(num):
for i in range(2, num):
if num % i == 0:
return False
return True
for i in range(m, n+1):
if find_prime(i):
print(i, end=' ')위의 방법이 있다.
하지만 위의 방법은 2중 반복문을 사용하므로 최소 \(O(N^2)\) 의 시간 복잡도를 갖게 된다.
다른 방식의 소수를 구하는 방법 중에 유명한 방법으로는
에라토스테네스의 체 방식이 있다. (위키피디아)
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
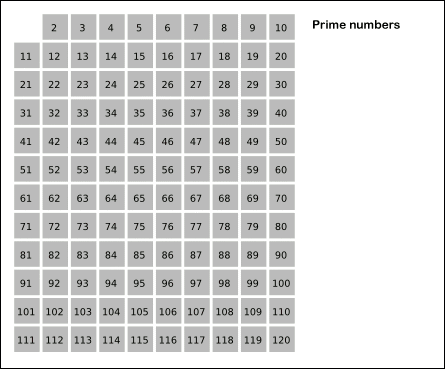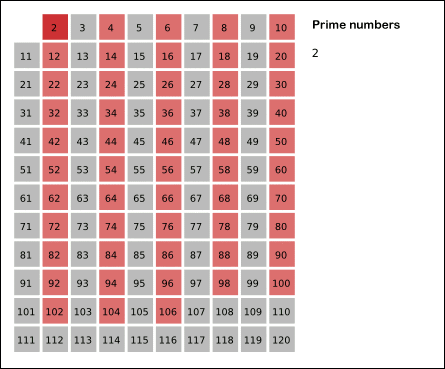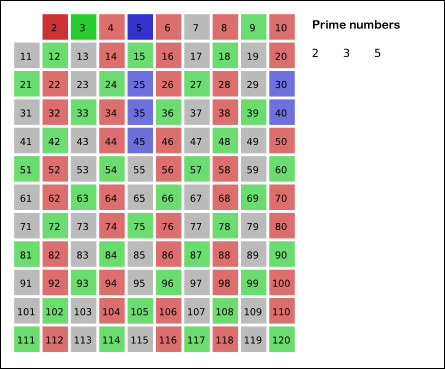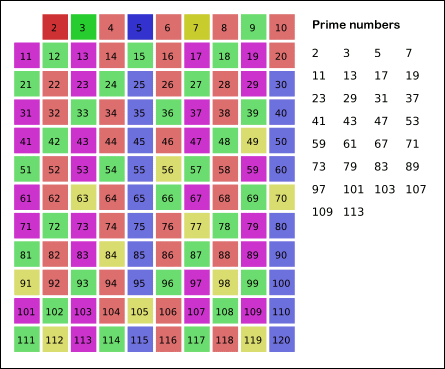
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
위의 알고리즘을 거쳐 완성된다.
코드로 보면
import sys
m, n = map(int, sys.stdin.readline().split())
isPrime = [1] * (n+1)
isPrime[0] = isPrime[1] = 0
for i in range(2, n+1):
if isPrime[i]:
for j in range(i*i, n+1, i):
isPrime[j] = 0
for i in range(m, n+1):
if isPrime[i]:
print(i, end=' ')
isPrime = [1] * (n+1) #모두 '참'인 형태로 주어진 0부터 주어진 값 까지의 배열 생성
isPrime[0] = isPrime[1] = 0 # 0과 1은 소수가 아니므로 0isPrime 배열은 각 자연수가 소수인지 아닌지를 판단하는 배열이다.
자연수 0과 1은 소수가 아니므로 0(거짓)으로 설정한다.
for i in range(2, n+1):
if isPrime[i]: #해당 수가 소수인지 확인
for j in range(i*i, n+1, i): #소수이면 해당 수의 배수를 모두 0(거짓)으로 변경
isPrime[j] = 0처음 반복문에서 해당 수가 참인지 거짓인지 확인 후
소수이면 해당 수의 모든 배수를 거짓으로 바꾼다.
앞선 예시의 예를 들어
2가 들어왔다면
2의 배수인 4, 6, 8, 10... 등은 모두 소수가 아니게 된다.
for i in range(m, n+1):
if isPrime[i]:
print(i, end=' ')이후 소수인 수들만 확인하여 출력한다.
에라토스테네스의 체 알고리즘 또한 소수인지 확인할 때 2중 반복문을 사용하여 \(O(N^2)\)의 시간 복잡도를 가질 것 같지만
확인할 때도 있고 안 할 때도 있으며
수가 커질수록 확인을 안 하는 경우가 늘어나기 때문에 \(O(N^2)\) 보다는 더 빠른 속도로 소수를 찾을 수 있게 된다.
시간 복잡도는 O(n log(logn))의 시간 복잡도를 갖는다.
'Algorithm > 백준' 카테고리의 다른 글
| [Python] 백준 2108번 - 통계학 (0) | 2022.10.31 |
|---|---|
| [Python] 백준 1966번 - 프린터 큐 (0) | 2022.10.30 |
| [Python] 백준 2839번 - 설탕 배달 (0) | 2022.10.28 |
| [Python] 백준 11651번 - 좌표 정렬하기 2 (0) | 2022.10.27 |
| [Python] 백준 7568번 - 덩치 (0) | 2022.10.24 |




댓글