https://www.acmicpc.net/problem/14500
14500번: 테트로미노
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다. 정사각형은 서로 겹치면 안 된다. 도형은 모두 연결되어 있어야 한다. 정사각형의 변
www.acmicpc.net
혼자 힘으로 풀었는가? O
알고리즘 분류
- 구현
- 브루트포스 알고리즘
문제
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.
- 정사각형은 서로 겹치면 안 된다.
- 도형은 모두 연결되어 있어야 한다.
- 정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.
정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.
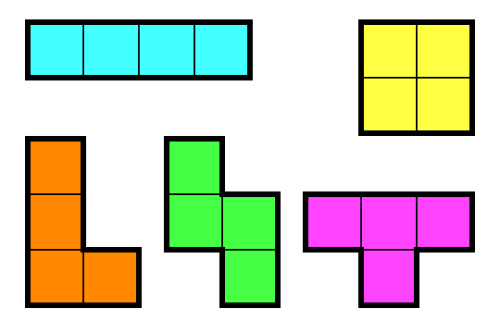
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.
테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.
테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.
입력
첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)
둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.
출력
첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.


역시 처음엔 문제이해부터가 쉽지 않았다.
뭐지? 테트리스 풀라는건가??
하지만 문제는 주어진 5가지 모형의 4칸의 조합으로 최댓값을 찾는 문제였다.
처음엔 이걸 어떻게 풀지.. 하고 고민을 했다. 그러고 방법이 도저히 떠오르지 않아 알고리즘 분류를 확인했고
브루트포스 알고리즘으로 풀면 된다고 해서 일단 브루트포스로 접근했다.
사실상 모든 경우의 수를 하나하나 확인하라는 뜻...
브루트포스
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
data = []
for _ in range(n):
data.append(list(map(int, input().split())))
val = 0
#위/오른쪽/아래/왼쪽 시계방향
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
def get_4x1(x, y, dir):
cnt = 0
for i in range(4):
nx = x + dx[dir] * i
ny = y + dy[dir] * i
if 0 > nx or 0 > ny or nx >= n or ny >= m:
return 0
cnt += data[nx][ny]
return cnt
def get_2x2(x, y):
nx = x + 1
ny = y + 1
if nx >= n or ny >= m:
return 0
cnt = data[x][y]
cnt += data[nx][y]
cnt += data[x][ny]
cnt += data[nx][ny]
return cnt
def get_L(x, y, dir):
cnt = 0
for i in range(3):
nx = x + dx[dir] * i
ny = y + dy[dir] * i
if 0 > nx or 0 > ny or nx >= n or ny >= m:
return 0
cnt += data[nx][ny]
c1 = c2 = 0
if dir % 2 == 0: #위나 아래방향이면
tmp1 = ny+1
if tmp1 < m:
c1 = data[nx][tmp1]
tmp2 = ny-1
if tmp2 >= 0:
c2 = data[nx][tmp2]
else:
tmp1 = nx+1
if tmp1 < n:
c1 = data[tmp1][ny]
tmp2 = nx-1
if tmp2 >= 0:
c2 = data[tmp2][ny]
if c1 == 0 and c2 == 0:
return 0
cnt += max(c1, c2)
return cnt
def get_Z(x, y, dir):
cnt = 0
for i in range(2):
nx = x + dx[dir] * i
ny = y + dy[dir] * i
if 0 > nx or 0 > ny or nx >= n or ny >= m:
return 0
cnt += data[nx][ny]
c1 = c2 = 0
if dir % 2 == 0: #위나 아래방향이면
left = ny-1
right = ny+1
if 0<= left:
c1 = data[nx][left]
nnx = nx+dx[dir]
if 0 <= nnx < n:
c1 += data[nnx][left]
else:
c1 = 0
if right < m:
c2 = data[nx][right]
nnx = nx+dx[dir]
if 0 <= nnx < n:
c2 += data[nnx][right]
else:
c2 = 0
else:
up = nx -1
down = nx+1
if 0 <= up:
c1 = data[up][ny]
nny = ny+dy[dir]
if 0<=nny<m:
c1 += data[up][nny]
else:
c1 = 0
if down < n:
c2 = data[down][ny]
nny = ny+dy[dir]
if 0 <= nny < m:
c2 += data[down][nny]
else:
c2 = 0
if c1 == 0 and c2 == 0:
return 0
cnt += max(c1,c2)
return cnt
def get_jk(x, y, dir):
cnt = 0
for i in range(2):
nx = x + dx[dir] * i
ny = y + dy[dir] * i
if 0 > nx or 0 > ny or nx >= n or ny >= m:
return 0
cnt += data[nx][ny]
tmpx = nx + dx[dir]
tmpy = ny + dy[dir]
if 0>tmpx or 0>tmpy or tmpx>=n or tmpy>=m:
return 0
cnt += data[tmpx][tmpy]
c1 = c2 = 0
if dir % 2 == 0: #위나 아래방향이면
left = ny-1
right = ny+1
if 0 <= left:
c1 = data[nx][left]
if right < m:
c2 = data[nx][right]
else:
up = nx -1
down = nx+1
if 0 <= up:
c1 = data[up][ny]
if down < n:
c2 = data[down][ny]
if c1 == 0 and c2 == 0:
return 0
cnt += max(c1, c2)
return cnt
sum = 0
for i in range(n):
for j in range(m):
case2 = get_2x2(i, j)
for k in range(4): #시계방향
case1 = get_4x1(i, j, k)
case3 = get_L(i, j, k)
case4 = get_Z(i, j, k)
case5 = get_jk(i, j, k)
sum = max(sum, case1, case2, case3, case4, case5)
print(sum)
5가지 모형의 모든 경우의 수에 대해서 조건을 확인하는 코드이다.
각 case1~5까지 알아보자.
case1
def get_4x1(x, y, dir):
cnt = 0
for i in range(4):
nx = x + dx[dir] * i
ny = y + dy[dir] * i
if 0 > nx or 0 > ny or nx >= n or ny >= m:
return 0
cnt += data[nx][ny]
return cnt단순한 방법이다.
주어진 칸부터 직선으로 4칸을 구하면 되기 때문에 반복문을 통해 처리해 주었다.
case2
def get_2x2(x, y):
nx = x + 1
ny = y + 1
if nx >= n or ny >= m:
return 0
cnt = data[x][y]
cnt += data[nx][y]
cnt += data[x][ny]
cnt += data[nx][ny]
return cntㅁ 모양은 2x2칸이 필요하므로 해당 칸의 범위만 확인한 후 값을 찾아주었다.
참고로

반복문을 보면 알 수 있겠지만 ㅁ 모양은 방향을 구 할 필요 없이 직사각형 내부에서 모든 경우의 수를 확인 가능하기 때문에
방향 반복문인 k 반복문을 통하지 않고 그전에 구해 줌으로써 불필요한 반복을 줄여주었다.
case3
def get_L(x, y, dir):
cnt = 0
for i in range(3):
nx = x + dx[dir] * i
ny = y + dy[dir] * i
if 0 > nx or 0 > ny or nx >= n or ny >= m:
return 0
cnt += data[nx][ny]
c1 = c2 = 0
if dir % 2 == 0: #위나 아래방향이면
tmp1 = ny+1
if tmp1 < m:
c1 = data[nx][tmp1]
tmp2 = ny-1
if tmp2 >= 0:
c2 = data[nx][tmp2]
else:
tmp1 = nx+1
if tmp1 < n:
c1 = data[tmp1][ny]
tmp2 = nx-1
if tmp2 >= 0:
c2 = data[tmp2][ny]
if c1 == 0 and c2 == 0:
return 0
cnt += max(c1, c2)
return cntL 모양은 직선으로 3칸 그 후 좌우 혹은 위아래 대칭으로 한 칸이 방향이 달라진다.
3칸까지는 직선과 동일하게 구해준 후
방향이 위아래일 때 한 칸은 좌우
방향이 좌우일 땐 한 칸은 위아래이기 때문에
해당값을 따로 구해준 후 가장 큰 값만 리턴해주었다.
case4
def get_Z(x, y, dir):
cnt = 0
for i in range(2):
nx = x + dx[dir] * i
ny = y + dy[dir] * i
if 0 > nx or 0 > ny or nx >= n or ny >= m:
return 0
cnt += data[nx][ny]
c1 = c2 = 0
if dir % 2 == 0: #위나 아래방향이면
left = ny-1
right = ny+1
if 0<= left:
c1 = data[nx][left]
nnx = nx+dx[dir]
if 0 <= nnx < n:
c1 += data[nnx][left]
else:
c1 = 0
if right < m:
c2 = data[nx][right]
nnx = nx+dx[dir]
if 0 <= nnx < n:
c2 += data[nnx][right]
else:
c2 = 0
else:
up = nx -1
down = nx+1
if 0 <= up:
c1 = data[up][ny]
nny = ny+dy[dir]
if 0<=nny<m:
c1 += data[up][nny]
else:
c1 = 0
if down < n:
c2 = data[down][ny]
nny = ny+dy[dir]
if 0 <= nny < m:
c2 += data[down][nny]
else:
c2 = 0
if c1 == 0 and c2 == 0:
return 0
cnt += max(c1,c2)
return cnt지그재그 모양은 2칸까진 직선, 이후 한 칸을 틀고 다시 직선이다.
L모양의 응용편이라 생각하면 편하다.
up/down, left/right로 다음 방향을 잡은 후
원래 진행하던 앞선 두 칸의 직진방향대로 그대로 향해주면 지그재그 방향의 값을 찾을 수 있다.
case5
def get_jk(x, y, dir):
cnt = 0
for i in range(2):
nx = x + dx[dir] * i
ny = y + dy[dir] * i
if 0 > nx or 0 > ny or nx >= n or ny >= m:
return 0
cnt += data[nx][ny]
tmpx = nx + dx[dir]
tmpy = ny + dy[dir]
if 0>tmpx or 0>tmpy or tmpx>=n or tmpy>=m:
return 0
cnt += data[tmpx][tmpy]
c1 = c2 = 0
if dir % 2 == 0: #위나 아래방향이면
left = ny-1
right = ny+1
if 0 <= left:
c1 = data[nx][left]
if right < m:
c2 = data[nx][right]
else:
up = nx -1
down = nx+1
if 0 <= up:
c1 = data[up][ny]
if down < n:
c2 = data[down][ny]
if c1 == 0 and c2 == 0:
return 0
cnt += max(c1, c2)
return cntㅗ ㅜ ㅓ ㅏ 모양의 값을 찾아야 한다.
jk로 한 이유는 ㅓㅏ 모양이라서... jk로 했다. 별 의미는 없다.
위와 동일하게 앞선 두 칸을 직진한 이후
두 번째 칸의 좌표를 기억해 두고 각각 한 칸 옆으로 갔을 때, 직진했을 때의 값을 합쳐서 리턴해준다.
DFS
문제를 다 푼 이후 다른 사람들은 어떤 방식으로 풀었나 검색을 해보았는데
visited로 방문흔적을 남기며 재귀를 이용한 DFS로 많이들 푼 것이다.
난 재귀가 약해서 직접 풀어보진 못했고 다른 사람의 코드를 참조하였다.
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
data = []
for _ in range(n):
data.append(list(map(int, input().split())))
val = 0
#위/오른쪽/아래/왼쪽 시계방향
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
visited = [ [0] * m for _ in range(n)]
def dfs(x, y, index, total):
global val
if index == 3:
val = max(val, total)
return
else:
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < m and visited[nx][ny] == 0:
if index == 1:
visited[nx][ny] = 1
dfs(x, y, index+1, total + data[nx][ny])
visited[nx][ny] = 0
visited[nx][ny] = 1
dfs(nx, ny, index+1, total+data[nx][ny])
visited[nx][ny] = 0
for i in range(n):
for j in range(m):
visited[i][j] = 1
dfs(i, j, 0, data[i][j])
visited[i][j] = 0
print(val)index == 3 을 확인하는 이유는 앞선 내 코드와는 달리 처음 dfs() 함수를 호출할 때부터 해당 좌표의 값을 가지고 출발했기 때문에 3칸만 움직이면 되기 때문에 index==3에서 리턴되는 것이다.
반복문 내부에서 index==1일 때 nx ny값을 사용하는 게 아닌 x, y로 dfs()를 재귀하는 이유는
ㅜㅗㅓㅏ 값을 찾기 위해서 index==1일 때 (위의 코드에서는 2칸 직진한 이후) 재귀를 호출하여 주는 것이다.
해당 코드는 눈으로 보고 이해하기는 쉽지 않으며 직접 실행하며 코드를 한줄한줄 읽다 보면 알 수 있는 것이
모든 방향을 재귀로 방향을 바꿔가면서 4칸에 해당하는 모든 경우의 수를 확인하며 돌아온다.
예를 들어서
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
으로 시작한다고 치면
처음엔
1 1 1 0
0 1 0 0
0 0 0 0
0 0 0 0
이후
1 1 1 0
0 0 0 0
0 0 0 0
0 0 0 0
1 1 0 0
0 0 0 0
0 0 0 0
0 0 0 0
까지 재귀로 돌아간다. 이후 index==1밑의 dfs()로 내려가지면서
1 1 1 0
0 0 0 0
0 0 0 0
0 0 0 0
다시 위의 상태가 되며 index = 2가 된다. 그 후
1 1 1 1
0 0 0 0
0 0 0 0
0 0 0 0
위와 같이 되며 index = 3이 되며 리턴으로 돌아온다.
돌아온 후 visisted[nx][ny] = 0을 거치면서 다시
1 1 1 0
0 0 0 0
0 0 0 0
0 0 0 0
로 변하고
상우하좌의 방향으로 넘어가기 때문에
상은 0 미만이라 안되며, 오른쪽은 방금 0으로 바뀌었고 그다음 방향인 아래로 내려가며
1 1 1 0
0 0 1 0
0 0 0 0
0 0 0 0
하면서 L모양까지 확인, 이후
1 1 0 0
0 0 0 0
0 0 0 0
0 0 0 0
다시 0으로 초기화
1 1 0 0
0 1 1 0
0 0 0 0
0 0 0 0
지그재그모양 확인
1 1 0 0
0 1 0 0
0 1 0 0
0 0 0 0
이후 아래로
1 1 0 0
1 1 0 0
0 0 0 0
0 0 0 0
마지막 반복문인 왼쪽으로 가면서 ㅁ 모양까지 확인, 이렇게 (0, 0)의 확인이 끝나게 된다.
마치 지렁이 게임? 처럼 머리의 방향을 계속 추가하면서 4칸이 될 때까지 모든 방향을 읽는다고 생각하면 된다.
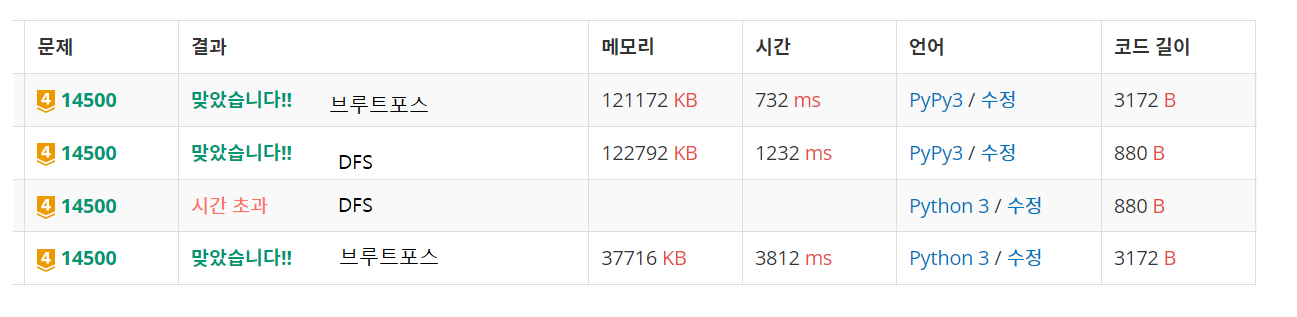
시간은 당연히 DFS가 잘 나올 줄 알았는데
브루트포스가 생각보다 빨랐다...
알 수 없는 시간복잡도의 세계...
아래는 내가 참고했던 반례들이다.
4 4
1 1 1 1
1 1 1 1
1 1 1 1
1 2 3 4
10
5 5
1 1 1 1 1
1 1 1 1 1
1 1 9 9 1
1 1 8 9 9
1 1 1 1 1
36
4 5
5 5 5 5 5
5 100 1 1 100
5 5 5 5 5
5 5 5 5 5
202
4 4
1 100 1 1
1 8 1 1
10 8 11 1
1 1 1 1
127
5 4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
4 4
5 1 1 5
2 1 1 2
2 1 1 2
1 1 1 1
12
6 10
3 3 6 4 1 4 8 5 3 2
9 5 1 2 4 1 9 9 5 5
2 5 1 2 3 3 3 7 6 4
1 6 5 6 4 7 4 7 7 4
3 8 5 9 6 4 2 6 1 1
6 3 3 7 1 2 2 2 8 4
33
4 4
0 0 0 0
0 0 0 0
0 0 0 0
1 2 3 4
4 4
0 0 0 1
0 0 0 2
0 0 0 3
0 0 0 4
4 4
0 0 0 0
0 0 0 0
0 0 1 2
0 0 3 4
4 4
0 0 0 0
0 0 1 0
0 0 2 0
0 0 3 4
4 4
0 0 0 0
0 0 0 0
0 1 2 3
0 4 0 0
4 4
0 0 0 0
0 0 1 2
0 0 0 3
0 0 0 4
4 4
0 0 0 0
0 0 0 0
0 0 0 1
0 4 3 2
4 4
0 0 0 0
0 0 0 1
0 0 0 2
0 0 4 3
4 4
0 0 0 0
0 0 0 0
0 1 0 0
0 2 3 4
4 4
0 0 0 0
0 0 2 1
0 0 3 0
0 0 4 0
4 4
0 0 0 0
0 0 0 0
0 1 2 3
0 0 0 4
4 4
0 0 0 0
0 0 0 1
0 0 2 3
0 0 4 0
4 4
0 0 0 0
0 0 1 0
0 0 2 3
0 0 0 4
4 4
0 0 0 0
0 0 0 0
0 1 2 0
0 0 3 4
4 4
0 0 0 0
0 0 0 0
0 0 3 4
0 1 2 0
4 4
0 0 0 0
0 0 0 1
0 0 2 3
0 0 0 4
4 4
0 0 0 0
0 0 1 0
0 0 2 3
0 0 4 0
4 4
0 0 0 0
0 0 0 0
0 0 1 0
0 2 3 4
4 4
0 0 0 0
0 0 0 0
0 1 2 3
0 0 4 0
4 6
1 2 3 4 1 2
3 4 1 2 3 4
1 2 3 6 7 2
1 7 2 1 0 0
20
5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
1 1 1 1 1
1 9 1 1 1
20
'Algorithm > 백준' 카테고리의 다른 글
| [Python][Java] 백준 2407번 - 조합 (0) | 2023.02.08 |
|---|---|
| [Python] 백준 16236번 - 아기 상어 (0) | 2023.02.07 |
| [Python] 백준 9019번 - DSLR (0) | 2023.01.06 |
| [Python] 백준 16928번 - 뱀과 사다리 게임 (0) | 2023.01.03 |
| [Python] 백준 10026번 - 적록색약 (0) | 2022.12.31 |




댓글