https://www.acmicpc.net/problem/11653
11653번: 소인수분해
첫째 줄에 정수 N (1 ≤ N ≤ 10,000,000)이 주어진다.
www.acmicpc.net
문제
정수 N이 주어졌을 때, 소인수분해하는 프로그램을 작성하시오
입력
첫째 줄에 정수 N (1 ≤ N ≤ 10,000,000)이 주어진다.
출력
N의 소인수분해 결과를 한 줄에 하나씩 오름차순으로 출력한다. N이 1인 경우 아무것도 출력하지 않는다.
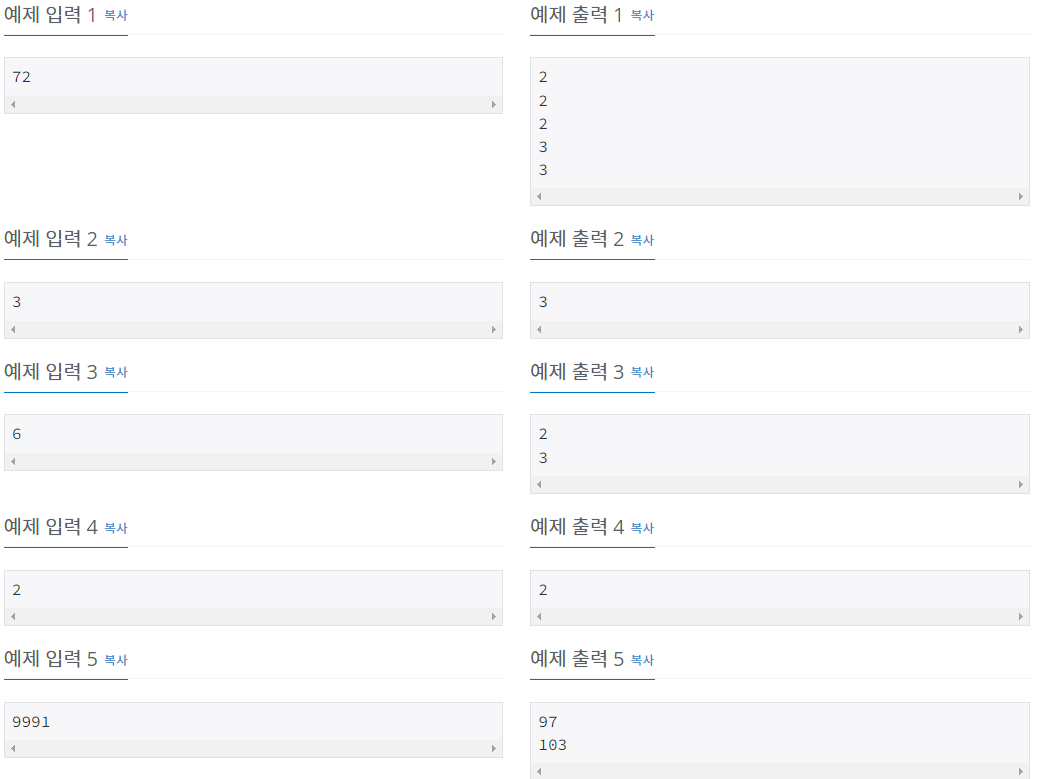
처음에는 굉장히 단순하게 풀었다.
나누는 값을 2부터 시작해서
나눠지지 않으면 +1을 해가면서 소인수분해를 찾았다.
n = int(input())
a = 2
if n != 1:
while True:
if n % a == 0:
print(a)
n = n // a
elif n % a != 0:
a += 1
if n == 1:
breakn 이 1이 되면 break로 탈출하게끔 돌려주었다.
하지만 실행하여보니 2192ms가 소모되었고 너무 느리다고 판단해서 코드를 더 경량화해보려고 하였다.
n = int(input())
a = 2
while a <= n:
if n % a == 0:
print(a)
n = n // a
else:
a += 1불필요한 if문을 줄여서 실행시간을 더 빠르게 해 보았다.
하지만 이렇게 해도 1488ms의 긴 시간이 소모되어서 어떻게 해야 더 빠른 시간에 실행하는지 궁금했다.
그래서 다른 사람의 정답 코드를 보고 내 방식대로 코드를 다시 작성해서 실행하였다.
n = int(input())
a = 2
while a <= int(n ** 0.5):
if n % a == 0:
print(a)
n //= a
else:
a += 1
if n > 1:
print(n)위의 코드로 실행하였을 때 시간은 68ms로 처음보다 32배가량 빨라졌으며
두 번째보다 21배가량 빨라진 속도가 나왔다.
이게 가능했던 이유는
반복 횟수를 제곱근만큼 줄였기 때문이다.
위의 예시중 입력값이 9991인 것을 예로 들면
9991은 97과 103 두 수로 소인수분해가 된다.
이 값이 나오기까지 a는 2부터 97까지 계속해서 a += 1을 반복하고 (여기까지는 모든 코드가 동일)
그다음 103이 나올 때까지 또 a += 1을 반복한다.
하지만 세 번째 코드의 경우 입력받은 값의 루트만큼 반복문을 돌려서 반복 횟수를 대폭 줄였다.
√9991 = 99.9549...
이므로 99까지만 계산하면 되며 남은 숫자가 1이 아니면 가장 마지막에 나와서 print(n)을 해주어 남은 소인수분해 값을 출력해준다.
위와 같은 방법으로 기존 첫 번째와 두 번째 코드처럼 끝까지 값을 찾아서 나눠주는 게 아닌
적당히 찾아서 나눠주는 방식으로 반복문 횟수를 대폭 줄여 빠른 실행시간을 얻었다.
'Algorithm > 백준' 카테고리의 다른 글
| [Python] 백준 1934번 - 최소공배수 (최소공배수, 최대공약수, 유클리드호제법) (0) | 2022.08.11 |
|---|---|
| [Python] 백준 1789번 - 수들의 합 (0) | 2022.08.10 |
| [백준] 2525번 오븐 시계 / 2530번 인공지능 시계 (0) | 2022.08.08 |
| [백준] 11021번 A+B -7 (0) | 2022.08.05 |
| [Python] 백준 10926번 ??! (0) | 2022.02.08 |


댓글