52. 자료구조 (B)
1. 자료구조
- 저장 공간의 효율성과 실행시간의 단축을 위해 사용

2. 배열 (Array)
- 크기와 형(Type)이 동일한 자료들이 순서대로 나열된 자료의 집합
- 반복적인 데이터 처리 작업에 적합
- 정적인 자료구조, 기억장소 추가 어려움
- 데이터 삭제시 빈 공간으로 남아있어 메모리 낭비 발생
3. 연속 리스트 (Contiguous List)
- 배열과 같이 연속되는 기억장소에 저장되는 자료구조
- 중간에 데이터를 삽입하기 위해 연속된 빈 공간이 있어야함
- 삽입삭제시 자료의 이동 필요
4. 연결 리스트 (Linked List)
- 자료들을 임의의 기억공간에 기억시키되, 자료 항목의 순서에 따라 노드의 포인터 부분을 이용해 서로 연결시킨 자료구조
- 연결을 위한 링크(포인터)가 필요하기 때문에 기억 공간의 이용 효율이 좋지 않음
- 접근속도 느리고, 연결이 끊어지면 다음 노드를 찾기 어려움
5. 스택 (Stack)
- 리스트의 한쪽 끝으로만 자료의 삽입, 삭제 작업이 이루어짐
- LIFO
- 저장할 공간이 없는데 삽입되면 Overflow
- 삭제할 데이터가 없는데 삭제하면 Underflow

6. 큐 (Queue)
- 리스트의 한쪽은 삽입, 한쪽은삭제
- FIFO
- 앞은 front, 뒤는 rear
7. 그래프 (Graph)
- 정점(Vertex)과 간선(Edge)의 집합으로 이루어짐
- 사이클이 없는 그래프를 트리라고 함
- 방향 그래프, 무방향 그래프
8. 방향/무방향 그래프의 최대 간선 수
- 방향 : n(n-1)
- 무방향 : n(n-1) / 2
53. 트리 (Tree) (C)

- 근노드 (Root Node) : 트리의 맨 위 / A
- 디그리 (Degree, 차수) : 각 노드에서 뻗은 가지 수 / A=3, B=2, C=1, D=3
- 단말 노드 (Terminal Node) = 잎 노드 (Leaf Node) : 자식이 없는 노드, 즉 Degree가 0인 노드 / K, L, F, G, M, I, J
- 비 단말 노드 (Non-Terminal Node) : 자식이 하나라도 있는 노드, 즉 Degree가 0이 아닌 노드 / A, B, C, D, E, H
- 조상 노드 (Ancestors Node) : 임의의 노드에서 근노드에 이르는 경로상에 있는 노드들 / M의 조상 노드는 H, D, A
- 자식 노드 (Son Node) : 어떤 노드의 다음 레벨 노드 / D의 자식 노드 : H, I, J
- 부모 노드 (Patrent Node) : 어떤 노드의 이전 레벨 노드 / E, F의 부모 노드는 B
- Level : 근노드의 level을 1로 가정한 후 어떤 level이 L이면 자식 노드는 L+1 / H의 레벨은 3
- 깊이 (Depth, Height) : 트리에서 노드가 가질 수 있는 최대 레벨 / 위 트리의 깊이는 4
- 숲(Forest) : 여러 개의 트리가 모여있는 것
- 트리의 디그리 : 노드들의 디그리 중 가장 많은 수 / A, D가 3개의 디그리를 가지므로 3이다.
54. 이진 트리(Tree) (A)
1. 이진 트리
- 차수(Degree)가 2 이하인 노드들로 구성된 트리
- 이진 트리의 레벨 i에서 최대 노드의 수는 $ 2^{i-1} $ 이다.
순회
- 전위 순회 (PreOrder)
- Root, Left, Right
- 뿌리 먼저 방문
- 중위 순회 (InOrder)
- Left, Root, Right
- 왼쪽 하위 노드 방문 후 뿌리 방문
- 후위 순회 (PostOrder)
- Left, Right, Root 순
- 하위 노드 모두 방문 후 뿌리 방
A
/ \
B C
/ \ \
D E F
/ / \
G H I
- 전위 순회 (Pre-order Traversal)
- 순서: A → B → D → E → G → C → F → H → I
- 설명: 루트(A)를 먼저 방문, 왼쪽 서브트리(B-D-E-G)를 방문, 그리고 오른쪽 서브트리(C-F-H-I)를 방문합니다.
- 중위 순회 (In-order Traversal)
- 순서: D → B → G → E → A → H → F → I → C
- 설명: 왼쪽 서브트리(D-B-G-E)를 먼저 방문, 그 다음 루트(A), 마지막으로 오른쪽 서브트리(H-F-I-C)를 방문합니다.
- 후위 순회 (Post-order Traversal)
- 순서: D → G → E → B → H → I → F → C → A
- 설명: 왼쪽 서브트리(D-G-E-B)를 먼저 방문, 그 다음 오른쪽 서브트리(H-I-F-C), 마지막으로 루트(A)를 방문합니다.
수식 표기법
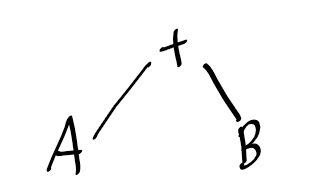
해당 A+B를 트리구조로 표현하면 위와 같다.
이를 전위(Prefix)수식, 후위(Postfix)수식으로 바꾸거나 중위(Infix)로 돌리는 방법.
Infix -> Prefix / Postfix

Postfix / Prefix -> Infix
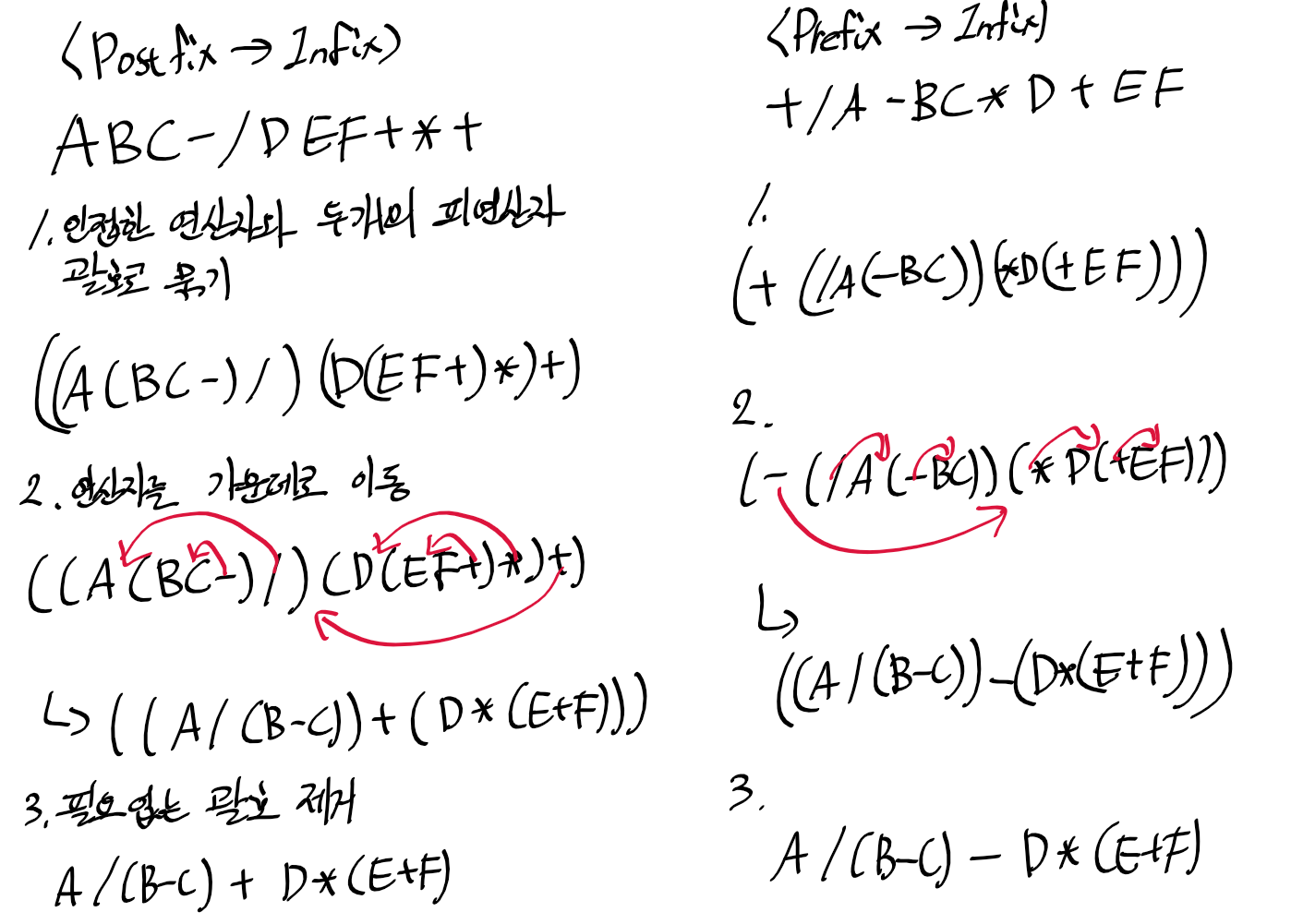
55. 정렬 (Sort) (A)
1. 삽입 정렬 (Insertion Sort)
- 가장 간단한 정렬 방식, 이미 순서화된 파일에 새로운하나의 레코드를 순서에 맞게 삽입시켜 정렬
- 평균, 최악 모두 O(N²)
1. 1번째 값과 0번째 값 비교하고 삽입 후 뒤로 밀기
2. 2번째 값을 0번째 값과 비교, 2번째 값을 1번째 값과 비교, 삽입 후 뒤로 밀기
3. 3번째 값을 0번째 값과 비교, 3번째 값을 1번째 값과 비교, 3번째 값을 2번째 값과 비교, 삽입 후 뒤로 밀기
...

2. 선택 정렬 (Selection Sort)
- n개의 레코드 중에 최소값을 찾아 첫 번째 레코드에 놓고, 나머지 n-1개 중에서 다시 최소값을 찾아 두번째 레코드 위치에 놓는 방식을 반복
- 평균 최악 모두 O(N²)
1. 0과 1~n-1을 계속 비교
2. 1과 2~n-1을 계속 비교
...
n. i와 i+1 ~n-1을 계속 비교
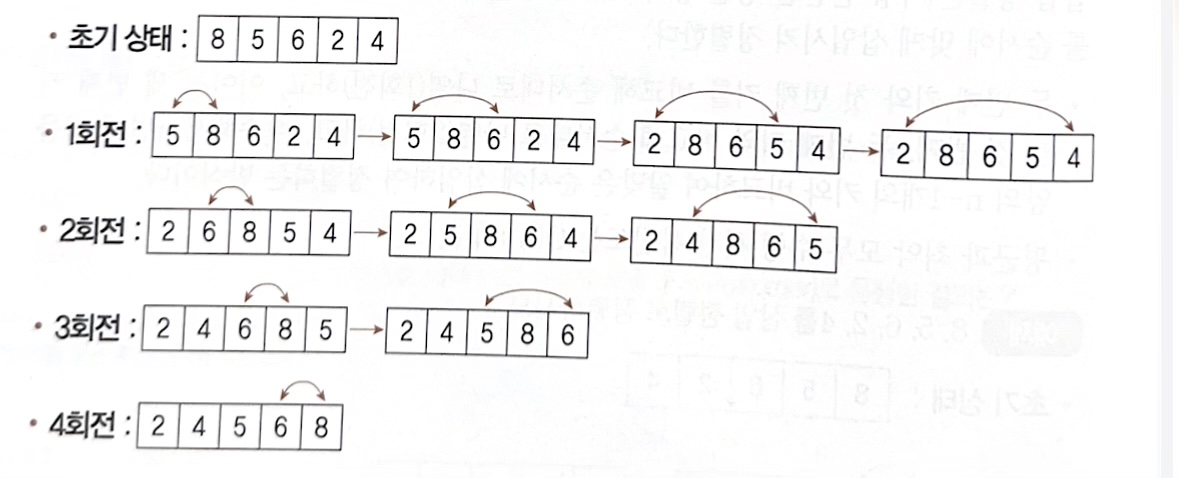
3. 버블 정렬 (Bubble Sort)
- 인접한 두 개의 레코드 값을 비교하여 크기에 따라 레코드 위치를 서로 교환
- 평균 최악 모두 O(N²)

4. 쉘 정렬 (Shell Sort)
- 어떤 매개변수의 값으로 서브 파일을 구성하고, 각 서브파일을 Insertion 정렬 방식으로 순서 배열하는 과정을 반복하는 정렬 방식
- 삽입 정렬(Insertion Sort)를 확장한 개념
- 평균 $ O(n^{1.5}) $이고, 최악 O(N²)
5. 퀵 정렬 (Quick Sort)
- 키를 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽으로 나눠서 과정을 반복하는 정렬 방식
- 시간 복잡도
- 평균 : O(nlog₂n)
- 최악 : O(N²)
- 정렬 중 가장 빠름
- 스택 사용
- 분할 정복 (Divide & Conquer)
- 피봇 (Pivot) 사용
6. 힙 정렬 (Heap Sort)
- 전이진 트리를 이용
- 평균과 최악 모두 O(nlog₂n)
7. 2-Way 합병 정렬 (Merge Sort)
- 이미 정렬되어 있는 두 개의 파일을 한 개의 파일로 합병
- 평균과 최악 모두 O(nlog₂n)
71, 2, 38, 5, 7, 61, 11, 26, 53, 42 를 2-way 합병 정렬로 정렬
1회 : 두 개씩 묶은 후 각각의 묶음 안에서 정렬
(71, 2) (38, 5) (7, 61) (11, 26) (53, 42)
↓
(2, 71) (5, 38) (7, 61) (11, 26) (42, 53)
2회 : 묶여진 묶음을 두 개씩 묶은 후 각각의 묶음 안에서 정렬
(2, 71, 5, 38) (7, 61, 11, 26) (42, 53)
↓
(2, 5, 38, 71) (7, 11, 26, 61) (42, 53)
3회
(2, 71, 5, 38, 7, 61, 11, 26) (42, 53)
↓
(2, 5, 7, 11, 26, 38, 61, 71) (42, 53)
4회
(2, 5, 7, 11, 26, 38, 61, 71, 42, 53)
↓
2, 5, 7, 11, 26, 38, 42, 53, 61, 71
8. 기수 정렬 (Radix Sort) = Bucket Sort
- 큐를 이용하여 자릿수별로 정렬
- 같은 수 또는 문자끼리그 순서에 맞는 버킷에 분배하였다가 버킷의 순서대로 레코드를 꺼내어 정렬
- 평균 최악 모두O(dn)
'정보처리기사 > 실기' 카테고리의 다른 글
| 정보처리기사 실기 5장 - 인터페이스 구현 (0) | 2024.07.05 |
|---|---|
| 정보처리기사 실기 4장 - 서버프로그램 구현 (0) | 2024.07.03 |
| 정보처리기사 실기 3장 - 통합 구현 (0) | 2024.07.03 |
| 정보처리기사 실기 2장 - 데이터 입출력 구현 (1) (1) | 2024.06.14 |
| 정보처리기사 실기 1장 - 요구사항 확인 (1) | 2024.06.11 |



댓글